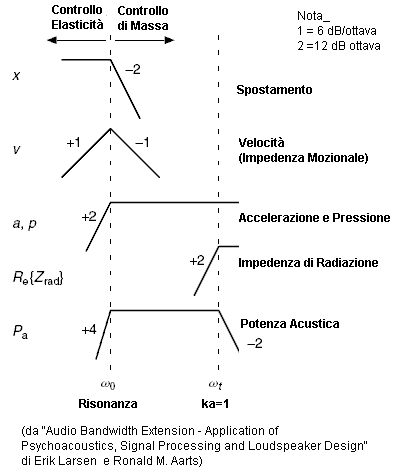
Accelerazione:

MB 7 luglio 2019

in Fisica l'accelerazione è la variazione della velocità (la derivata della velocità rispetto al tempo). Per quanto riguarda un altoparlante dinamico,nella regione dove ka<1, la pressione generata dal moto del diaframma è proporzionale alla sua accelerazione. Infatti per passare dallo spostamento alla pressione si deve derivare due volte (come mostrato nello schema che segue).

Dal punto di vista cinematico il moto del diaframma soggetto ad una oscillazione sinusoidale (armonica) di ampiezza X0 vale:

x(t) = X0 cos (wt)

t= tempo w = pulsazione = 2pf f = frequenza X0 = ampiezza massima

Per ottenere la velocità si deriva rispetto al tempo ottenendo (si noti che frequenza fissa X0 è una costante):

v(t) = - X0 w sin (wt)

e per ottenere l'accelerazione si deriva ancora una volta:

a(t) = - X0 w² cos (wt)

Prediamo un woofer con spostamento massimo di 6 mm (0.006 metri), che oscilla a 30 Hz. Calcoliamo spostamento, velocità ed accelerazione massima:

x_max = 0.006 m

v_max = 0.006 (2 p 30) = 1.13 m/s

a_max = 0.006 (2 p 30)² = 213.17 m/s²

Lo spostamento vale 6 mm, la velocità è ben minore della velocità del suono (1.13 contro 344 m/s) mentre l'accelerazione è oltre 20 volte maggiore dell'accelerazione di gravità (231 contro 9.6 m s^-2).

A parità di SPL prodotto lo spostamento si riduce di quattro volte per ogni raddoppio della frequenza quindi l'accelerazione rimane praticamente costante al crescere della frequenza (per risposta in frequenza piatta).

Infatti a 60 Hz risulta ancora:

a_max = (0.006/4) (2 p 30x2)² = (0.006/4) 4 (2 p 30)² = (0.006) (2 p 30)² = 213.17 m/s²

L'accelerazione massima si registra nel passaggio per lo zero (posizione di equilibrio).

Le ipotesi alla base delle equazioni di d'Alembert stabiliscono che il moto è lineare se l’attrito dipende solo dalla velocità e finché la velocità non supera i 2 metri al secondo.

Se prendiamo le espressioni di X_max, V_max e a_max e le moltiplichiamo per SD(superficie dell’altoparlante) otteniamo le espressioni dello spostamento volumetrico SD, dello spostamento di volume e della accelerazione di volume

SV = SD x_max = SD 0.006 m

VV = SD v_max = SD 0.006 (2 p 30) = 1.13 m/s

AV = SD a_max = SD 0.006 (2 p 30)² = 213.17 m/s²

Si vede così che aumentando SD, a parità di SPL lo spostamento richiesto diminuisce e diminuiscono, in proporzione, anche la velocità e l’accelerazione richiesta.