Glossario

Altoparlante: modello Scanspeak

Lo scopo del modello è calcolare la velocità del diaframma che (moltiplicata per la resistenza di radiazione) fornisce la potenza acustica emessa.

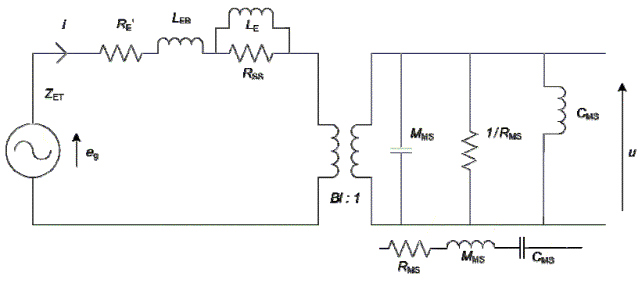
Il modello elettromeccanico dell’altoparlante dinamico si compone di due sezioni: elettrica (a sinistra) e meccanica(a dstra).

Per semplicità la massa di radiazione è inglobatanella massa dell’apparato mobile e il carico del cabinet (in sospensione pneumatica) è inglobato nella elasticità delle sospensioni.

L’induttanza propria della bobina mobile, a causa delle correnti di Focault che percorrono il polo centrale, non è costante e l’impedenza non cresce di 6 dB per ottava come nelle bobine avvolte in aria. Questo è il primo problema. Per risolverlo già da molti anni si usano circuiti RL per migliorare l’approssimazione (vds Kef e altri).

Sul lato elettrico, invece si osserva il seguente fenomeno: quando viene aggiunta una massa al diaframma il picco di risonanza a si sposta a frequenza più bassa (cone atteso) ma diminiusce anche di ampliezza (fenomeno non atteso). Ricordiamo che uno dei metodi per la misura dei parametri dell’altoparlante è qullo della “massa aggiunta”. L’effetto appena descritto è completamente assente nel modello che utilizza solo Mms, Cms e Rms indipendenti dalla frequenza.

Modello classico con variante Kef

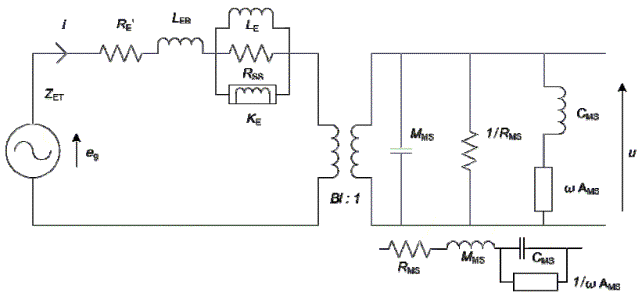
Gli ingegneri della Scanspeak hanno preparato un modello equivalente poco più complicato di quello canonico che contiene due elementi in più: una semi induttanza (per modellare la induttanza della bobina mobile) e una ammettenza reale ma dipendente dalla frequenza (w Ams) in serie all’elemento elastico.

In sostanza l’elemento meccanico elastico prevede un elemento dissipativo in parallelo che diminuisce al crescere della frequenza. Il duale elettrico dell’elemento elastico prevede un elemento resistivo in serie il cui valore aumenta con la frequenza.

Modello proposto da Scanspeak con due elementi dipendenti dalla frequenza

Parametri lato Elettrico	simbolo	valore	unità
Resistenza	Re'	3.35	M
Induttanza libera (Free inductance)	Leb	0.0580	mH
Induttanza legata (Bound inductance)	Le	0.444	mH
Semi induttanza (Semi-inductance)	Ke	0.0489	sH
Resistenza in parallelo (Shunt resistance)	Rss	1813	M

Parametri lato Meccanico
Fattore di forza (Force Factor)	Bl	5.44	Tm
Massa mobile(Moving mass)	Mms	10.4	g
Complianza (Compliance)	Cms	1.23	mm/N
Resistenza Meccanica (Mechanical resistance)	Rms	0.274	kg/s
Ammettenza (Admittance)	Ams	0.206	mm/N

http://www.scan-speak.dk/toolbox.htm

In this spreadsheet the calculation of the impedance of the semi-inductor looks like this:

First – the semi-inductor value is like Ke = xx semi-Henry (e.g. 0,1 sH)

Semi-induttanza Z(Ke) Ke (jw)^1/2 in semiHenry o sH

Parte reale

Ke * sqrt ( w / 2 )

Parte immaginaria

Ke * sqrt ( w / 2 )

La funzione impower di Excel calcola la potenza di un numero complesso come segue:

where:

and:

Richiami sui numeri complessi

Dato il numero complesso

$z = |z|(cos \theta + i sen \theta )\,\!$

$z^n = |z|^n ( cos(n\theta) + i sen(n\theta) )\,\!$

dove:

$(\cos x + i \, \sin x)^n = \cos (nx) + i \, \sin (nx)$

Dato il numero complesso in forma polare

$z = re^{i\theta} \,\!$ elevato a potenza diventa $z^n = r^ne^{ni\theta} \,\!$

Per quanto riguarda l’estrazione di radice, ogni numero complesso ha esattamente n radici n-esime: non esiste un modo univoco di definire la radice quadrata di un numero complesso.

Parametri lato Elettrico

Parametri lato Meccanico