Dispersione di alcuni array di altoparlanti

Mario Bon - 6 febbraio 2017

Un Array di altoparlanti è formato sostanzialmente da un certo numero di altoparlanti montati in colonna (anche più colonne affiancate).

Esempio di diffusore commerciale a tre vie che impiega array verticali.

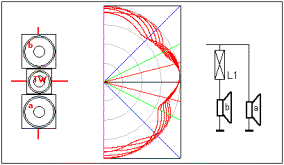
Configurazione minima:due altoparlanti

Dispersione verticale di due altoparlanti in parallelo ed in semiparallelo

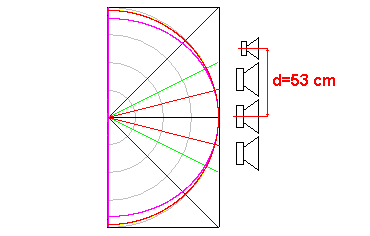
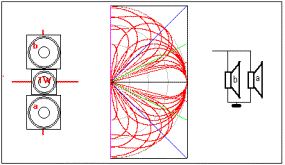
Configurazione con più altoparlanti

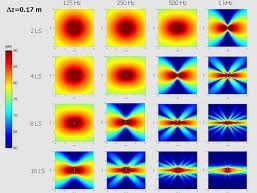
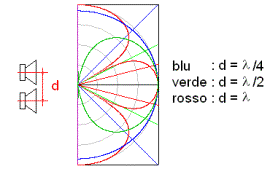
Le caratteristiche dell’array verticale dipendono dalla distanza tra le sorgenti. Anche se tale distanza è inferiore alla lunghezza d’onda gli array, in campo lontano, producono fronti d’onda sferici.

Il problema degli array lineari a colonna è la differenza di distanza tra la sorgente più lontana e quella più vicina al punto di ascolto (che genera interferenza). L’altro problema è la variazione del livello in asse in funzione della distanza:

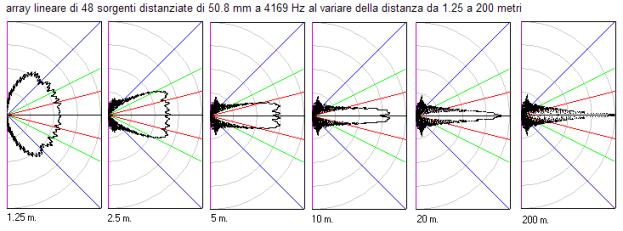
Questa sorgente lineare è alta poco più di 2.4 metri. Si vede bene come l’SPL in asse dipenda dalla distanza di misura. A 200 metri il microfono si trova in campo lontano. A 20 metri il microfono è ancora in campo semivicino.

La pressione in asse, a 2.5 metri, è circa 15 dB più bassa di quanto sarebbe se gli altoparlanti si sommassero in fase.

Riducendo la dimensione dell’array si può anche aumentare la banda passante riprodotta.

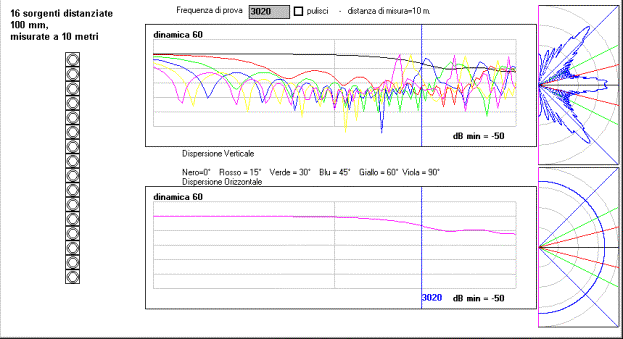
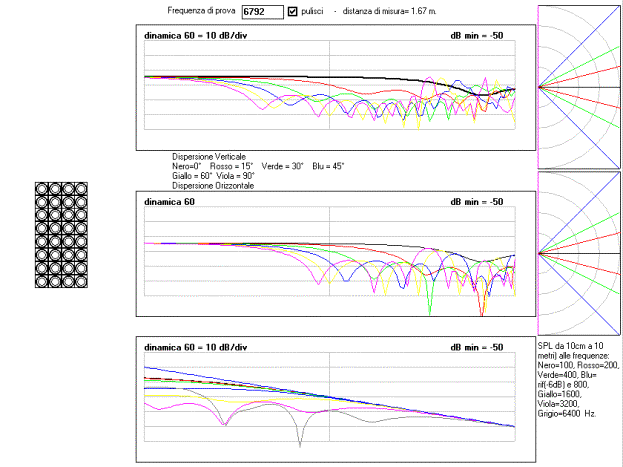
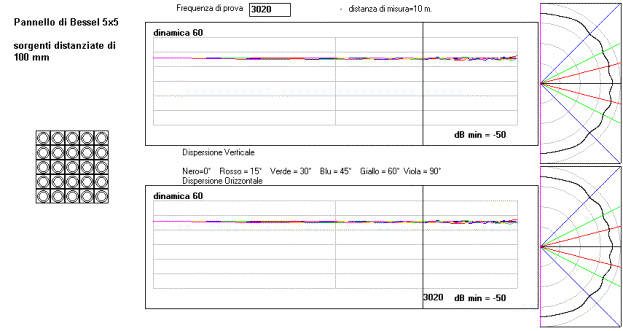
una colonna di 16 sorgenti uguali distanziate 100 mm misurata a 10 metri a 3020 Hz

Si noti che la risposta in frequenza in asse (in nero sul 1° grafico ed in viola nel 2° grafico) perde 5 dB sulle alte frequenze. Questa attenuazione è dovuta alla dimensione dell’array.

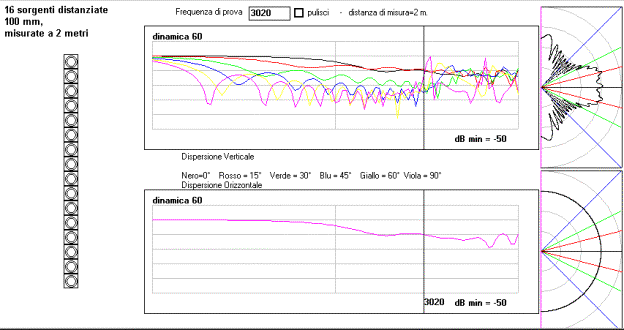
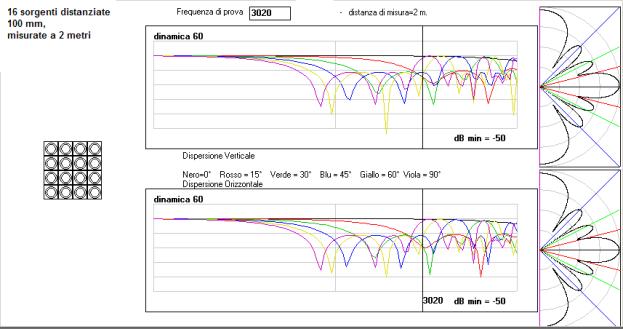
Come sopra ma misurata a 2 metri. La risposta in frequenza si attenua di 5 dB a frequenza più bassa. Il problema è la differenza di percorso tra la sorgente più vicina e quella più lontana all’ascoltatore.

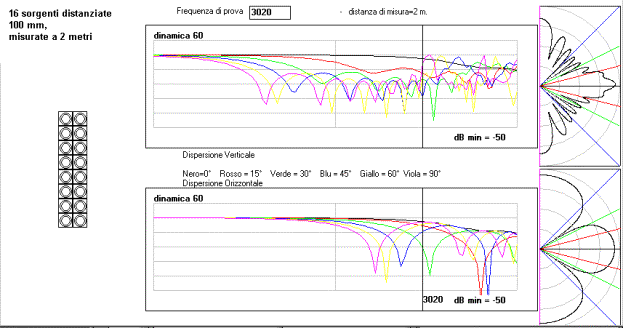
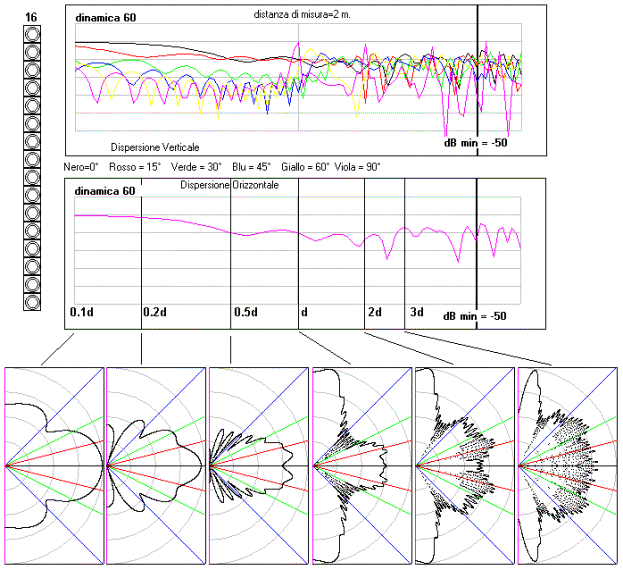
come sopra ma l’array è su due colonne. La risposta in frequenza si attenua di meno perché la differenza di distanza tra le sorgenti è diminuita. Aumenta la direttività sul piano orizzontale (Da una certa frequenza in su). I lobi verso l’ato e verso il basso sono aumentati.

Array su 4 colonne. Ora la distanza tra le sorgenti è minima, l’interferenza è diminuita e la risposta in frequenza è molto meno attenuata. La dispersione sul piano orizzontale e verticale è la stessa.

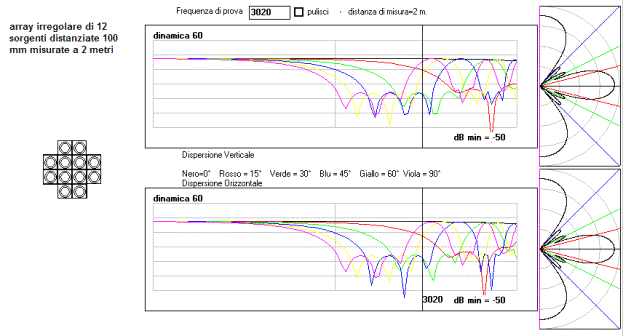
questo è l’array da 16 dove sono state escluse le sorgenti ai vertici (le più lontane). La risposta in frequenza in asse si appiattisce ulteriormente.

Questo è un pannello di Bessel di ordine 5x5 (sorgenti distanziate di 100 mm.). La simulazione riguarda il campo lontano. La dispersione verticale ed orizzontale sono uguali e non si osservano fenomeni di interferenza completamente distruttiva. La risposta in frequenza presenta lievi variazioni ma è sostanzialmente piatta.

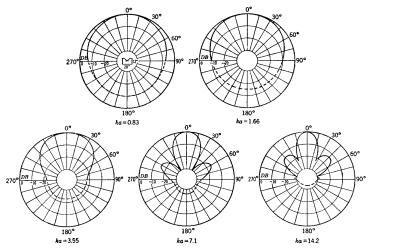
La dispersione è molto simile a quella della sorgente singola. La risposta impulsiva non può essere perfetta a causa della interferenza di sorgenti poste a distanze diverse.

Questi diagrammi polari partono dal presupposto che le sorgenti siamo delle sfere pulsanti puntiformi. In realtà le sorgenti reali hanno una dimensione finita e “stringono” la dispersione al crescere della frequenza. Tuttavia a distanza sufficiente la dimensione della singola sorgente è meno importante ed acquista sempre più importanza la dimensione dell’array.

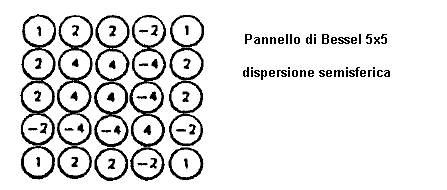
Ampiezza e fase relativa delle sorgenti nel pannello di Bessel a dispersione semisferica. Si noti che solo 3 su 5 colonne producono potenza acustica (le sorgenti nelle colonne 3 e 4 sono in controfase). Questo array, quindi, non può essere efficiente.

Ampiezza e fase relativa delle sorgenti nel pannello di Bessel ottimizzato solo per la dispersione verticale (5 colonne uguali).

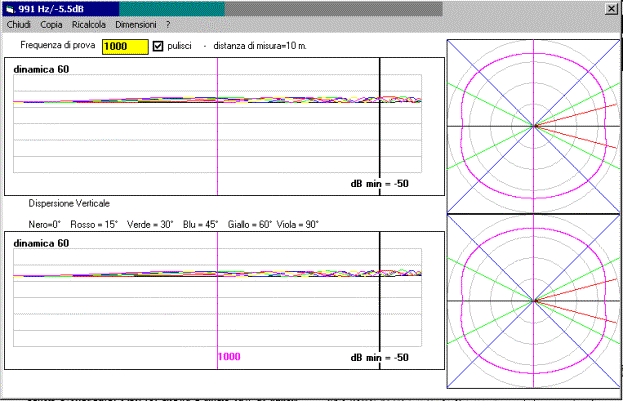
Risposta di un pannello di Bessel 3x3 a 1000 Hz.

I Pannelli di Bessel non sono l’unico modo per estendere la dispersione di un array di altoparlanti:

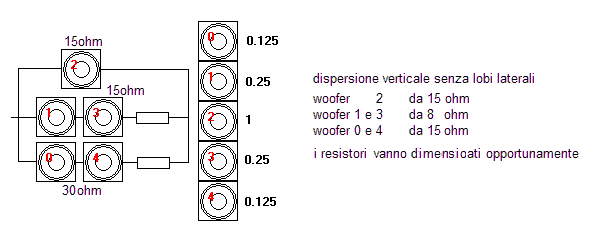
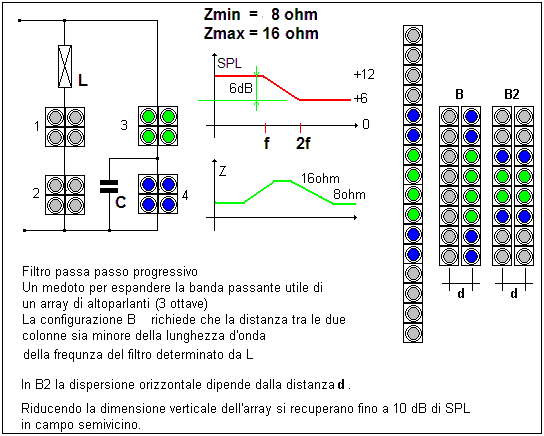
Array con filtri progressivi passivi

I filtri progressivi consentono di estendere la dispersione verticale di un array consentendone l’uso anche con il punto di ascolto più vicino.

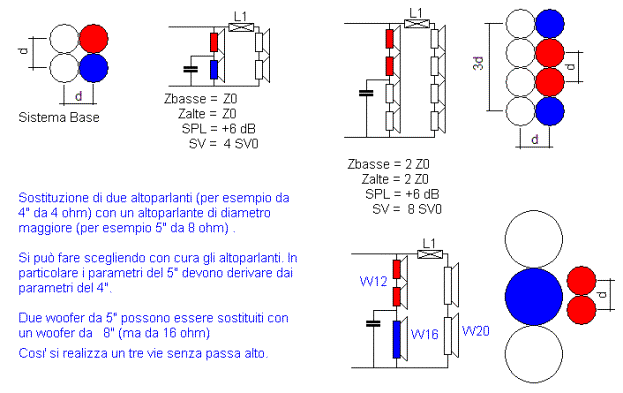
Filtro progressivo alternativo con 4 e 8 altoparlanti e la versione con altoparlanti con diametro diverso. In pratica due woofer vengono sostituiti dal un woofer equivalente (da realizzare con qualche accortezza in più).

Filtro progressivo alternativo con 16 altoparlanti

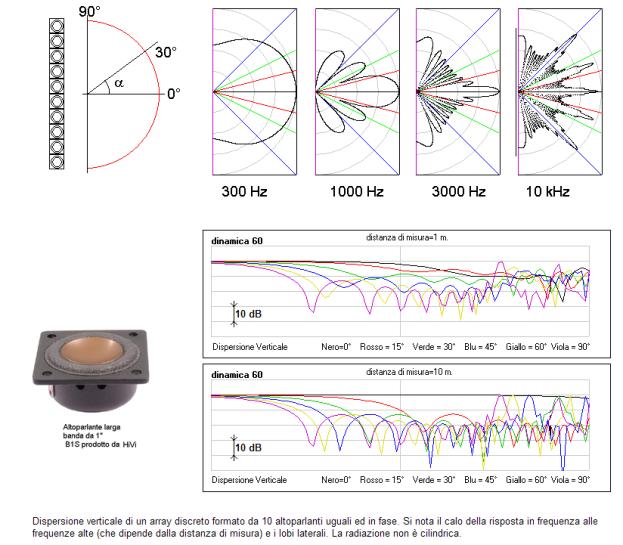
Un noto teorema stabilisce che la dispersione di un array di sorgente è pari al prodotto della dispersione della singola sorgente per la dispersione di un array di sorgenti puntiformi.