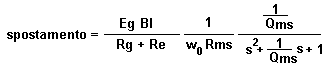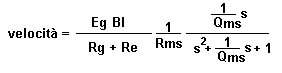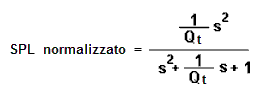TEB o cassa chiusa

Totally Enclosed Box = cassa completamente chiusa
detta anche sospensione pneumatica

La cassa chiusa è il tipo di carico più semplice da realizzare e si basa sulla soppressione dell’onda emessa dalla faccia posteriore del woofer.

L’impedenza di radiazione di un altoparlante in cassa chiusa, in campo libero, si può approssimare:

a bassissima frequenza: come una sfera pulsante ed emette onde sferiche (per ka << 1)

a bassa frequenza: come un pistone rigido montato su una sfera o alla fine di un lungo tubo.

La scelta della approssimazione dipende dalle dimensioni del cabinet e del pannello frontale.

Quando le dimensioni del pannello frontale diventano paragonabili con la lunghezza d’onda del suono emesso le semplificazioni non valgono più. Quando la frequenza è abbastanza alta l’altoparlante si comporta come se fosse montato su uno schermo infinito (ciò avviene quando la dispersione dell’altoparlante è minore di 180°).

Nel passaggio da funzionamento su spazio inero a mezzo spazio la potenza emessa raddoppia quindi è normale che, in camera anecoica, la risposta in frequenza di un altoparlante in TEB presenti un andamento crescente verso le alte frequenze. Questo incremento è limitato dalla induttanza della bobina mobile e incrementato dalla forma conica del diaframma (che tende a comportarsi come una tromba)

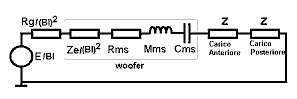
Circuiti equivalenti di un woofer in aria L’impedenza di carico, posteriore ed anteriore deve apparire in serie all’impedenza meccanica dell’altoparlante.

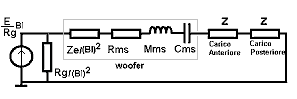
Circuiti equivalenti di un woofer in aria In questo circuito equivalente il generatore di forza è stato sostituito da un generatore di velocità il cui equivalente elettrico è un generatore di tensione (un amplificatore).

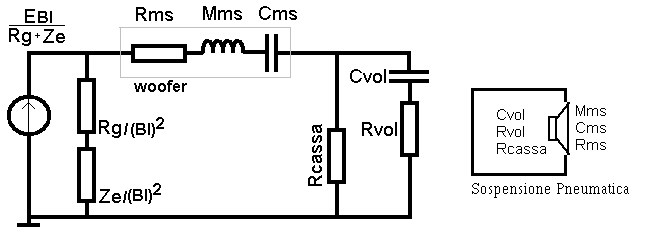
Circuito meccanico equivalente di un woofer in cassa chiusa con Rvol = perdite nel volume della cassa Rcassa=perdite per fessurazione

Circuito equivalente dell’impedenza di un woofer in cassa chiusa che tiene conto di tutti gli elementi presenti nel circuito equivalente precedente. In genere Rcassa non è presente. Le dipende dalla frequenza e comprende anche l’effetto delle correnti di perdita nel polo centrale.

Risolvendo i circuiti equivalenti si ottengono le espressioni per calcolare lo spostamento e la velocità.

Nelle figure che seguono Qms rappresenta il fattore di merito meccanico totale che tiene conto anche delle perdite nel volume.

Lo stesso vale per Rms, w₀ è la pulsazione del woofer in cassa.

in cassa chiusa l’elasticità della cassa si somma aquella del woofer e w0 aumenta quindi lo spostamento diminuisce.	Queste a sinistra sono le espressioni per lo spostamento e la velocità dell’apparato mobile di un woofer dinamico. s= j (w/w0) (variabile complessa) w0 = pulsazione del woofer =2pf0 f0 = frequenza di risonanza del woofer w = 2pf Lo spostamento va (quasi) come l’inverso del quadrato della frequenza quindi un altoparlante dinamico produce, in prima approssimazione, potenza acustica costante sulla banda passante utile (per valori di ka minori di uno).
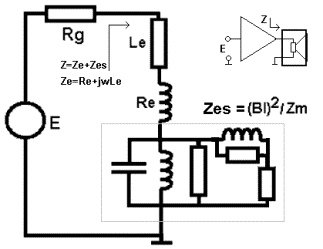
Per tenere conto dall’induttanza della bobina mobile basta sostituire Re con Ze. Espressioni valide per woofer in aria libera e cassa chiusa.

	Queste a sinistra è l’ espressioni normalizzata per l’ SPL prodotto da un woofer dinamico caricato in cassa chiusa valida a bassa frequenza e su schermo infinito. Come si vede l’SPL è proporzionale all’accelerazione del diaframma.
La funzione di trasferimento corrisponde ad un passa alto del secondo ordine dominato da Qt (Qt = fattore di merito totale che tiene conto di Qms, Qes e del Q del cabinet) Si devono quindi distinguere uno slew-rate elettrico e uno slew-rate meccanico

Data la funzione di trasferimento si determina la risposta impulsiva che, per fattori di merito inferiori a 0. 7, è la migliore che si possa ottenere rispetto a qualsiasi altro tipo di carico. In particolare si tratta di una funzione a fase minima. I sistemi aperti (dipolo, linea di trasmissione e il reflex al di sotto della Fb) non sono sistemi a fase minima e la risposta impulsiva è la somma di almeno due impulsi ritardati. Che poi questo abbia un effetto relativo all’ascolto, è un’altra storia. Questo è quanto si evince dai modelli basati su ragionamenti validati e condivisi.

Se si desidera la miglior risposta possibile (fase minima) si deve utilizzare un woofer in cassa chiusa.

Ci sono religioni i cui dogmi enunciano “verità” alternative: si tratta di religioni che, come tali, si basano su ragionamenti euristici non validati.

Per ottenere il livello SPL si deve moltiplicare la velocità del diaframma al quadrato per la parte reale dell’impedenza di radiazione (si assumo il modello di un pistone rigido). Tale espressione è valida per ka < 1 e fintantoché la profondità del cono è minore della lunghezza d’onda frequenza considerata. In sostanza si accettano una serie di semplificazioni perché questo modello deve simulare il funzionamento del woofer fino a 200-300 Hz. Tale limite è ampiamente sufficiente per woofer fino a 10” di diametro nominale.

Per woofer di diametro superiore (12”, 15”, ecc.) il limite della approssimazione si ferma a frequenze inferiori

Diametro nominale	Superficie di radiazione	Frequenza limite per ka=1
3.5”	32 cm^2	1715 Hz
4”	50 cm^2	1372 Hz
5”	80 cm^2	1085 Hz
5”	104 cm^2	951 Hz
7”	126 cm^2	864 Hz
7”	132 cm^2	845 Hz
8”	220 cm^2	654 Hz
8”	230 cm^2	640 Hz
10”	330 cm^2	534 Hz
10”	363 cm^2	510 Hz
12“	550 cm^2	413 Hz
15“	900 cm^2	323 Hz

Dalla tabella qui sopra appare chiaro che i woofer oltre 10“ di diametro nominale non sono adatti a riprodurre le frequenze medie a meno non adottino soluzioni particolari (per esempio un coni corrugato).

Stando a quanto si legge in rete un cono corrugato da 15” pollici dovrebbe avere indice di direttività costante (!) cosa evidentemente non vera.

Si tenga anche presente che l’effetto coincidenza, nei coni in carta, si verifica attorno a 700 Hz. Nello stesso range d frequenze si trovano le risonanze del rim e nei woofer da 8”-10” anche i primi break-up della membrana. Tutti questi fenomeni possono quindi cadere nello stesso intorno di frequenze e provocare gravi irregolarità nella risposta (sia sotto forma di risonanze che di interferenza).

L’effetto coincidenza può essere evitato utilizzando diaframmi in metallo (alluminio o magnesio). I diaframmi in titanio o in ceramica sono diagrammi di alluminio sul quale viene depositato (per vaporizzazione) un sottilissimo strato di titanio o ceramica (in pratica cambia il colore e poco altro).