Volume

24 maggio 2018

Il volume è lo spazio delimitato da una superficie chiusa. Quello che va precisato è il concetto di volume nell’ambito delle analogie elettro-meccaniche. Il volume, per poter essere modellizzato con una elasticità o un condensatore, deve avere delle caratteristiche:

- le dimensioni devono essere minori della lunghezza d’onda in modo che al suo interno non si formino onde stazionarie

- le dimensioni non devono essere troppo diverse tra loro

per esempio un parallelepipedo non deve essere troppo “schiacciato” altrimenti diventa una fenditura e non deve essere troppo allungato altrimenti diventa un condotto (un tubo).

Per capire se un volume è un “volume” si valuta il rapporto tra le misure del volume stesso e della superficie che lo delimita. Il solido geometrico con il volume maggiore in rapporto alla superficie è la sfera seguito dal cubo. In sostanza un volume deve avere un rapporto tra volume e superficie non troppo diverso da quello di una sfera o di un cubo. In tal caso si comporta come una molla o come un condensatore per frequenze la cui lunghezza d’onda è inferiore ad un ottavo della dimensione massima.

Frequenza	Lunghezza d’onda l	l/8
50 Hz	6.88 metri	86.centimetri
100 Hz	3.44 metri	43 centimetri
150 Hz	2.29 metri	28.6.centimetri
200 Hz	1.72 metri	21.centimetri

Dalla tabella si vede che solo volume relativamente piccoli si comportano come tali. In sostanza un cubo con 50 centimetri di lato si comporta come u “volume” solo fino a 50 Hz. Questo non è un fatto trascurabile che costringe a considerare con attenzione il calcolo dei sistemi reflex di volume superiore a 125 litri.

I criteri per scegliere i rapporti dimensionali di un cabinet per un altoparlante sono gli stessi che si utilizzano per determinare i rapporti dimensionali di una stanza. Si può quindi far riferimento ai criteri di Bonello. 

L’impedenza acustica di ingresso di un tubo rigidamente chiuso vale:

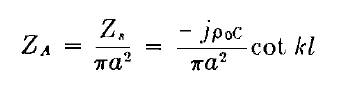
per 0.05 Sqr(f)>raggio>10/f dove f è la frequenza e il raggio è il raggio del tubo.

Raggio	Freq. minima	Freq Massima
15 centimetri	9 Hz	66 Hz
8.3 centimetri	2.75 Hz	120 Hz
5 centimetri	1 Hz	200 Hz

Nota: per i tubi di diametro inferiore la massa può essere fino a tre volte maggiore e si deve tenere conto delle perdite resistite che appaiono in serie.

Anche in questo caso si vede come i limiti del modello siano abbastanza ristretti: il limite verso le basse frequenze non è un problema mentre lo è la limitazione della frequenza superiore.

Se sviluppiamo la cotangente si serie di Taylor otteniamo:

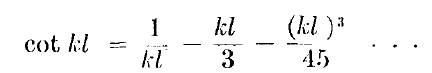
Se teniamo i primi due termini e sostituiamo otteniamo, per l’impedenza meccanica l’espressione:

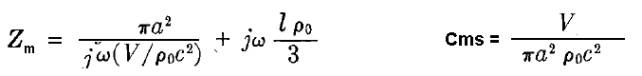
Questa rappresenta un condensatore (molla) in serie ad una induttanza (massa).

Per un volume chiuso generico la massa dipende dalla forma cabinet. Per volumi non troppo grandi e non troppo diversi da un tubo si può porre L = V/S dove è la sezione del cabinet.

La cosa rilevante è che, ove valga il modello a parametri concentrat, anche un volume chiuso presenta all’altoparlante una massa di carico che si somma alla massa del diaframma.

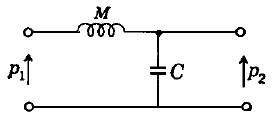
	Circuito meccanico equivalente di un tubo corto e chiuso ad una estremità
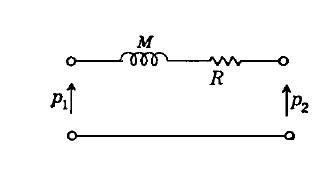
	Circuito equivalente di un tubo chiuso di piccolo diametro con perdite resistite in serie Le perdite dipendono dalla radice quadrata della frequenza (aumentano con la frequenza) ma diminuiscono con il raggio. In realtà un minimo d perdite è sempre presente (attrito e conduzione termica sulle pareti)