Forza di una sorgente

Indicata con Q. Per una sorgente è il prodotto della superficie SD moltiplicata per la velocità della superficie della sfera U_0.Per la sfera pulsante la superficie SD= 2 p a² e la forza vale

Q₀ =. SD U₀ = 4 p a² U₀ ovvero U₀ = Q₀/SD

La sorgente puntiforme non ha dimensioni.

La sorgente sferica ha dimensioni e la relazione tra pressione e velocità vale:

U₀ =velox = p /Za(kr)

p =Za(kr) velox = Za(kr) U₀ =Za(kr) Q /(4 p r²)

dove Za(kr) è l’impedenza di radiazione che dipende dalla frequenza e dalla distanza.

Impedenza specifica = Za(kr)=rc jkr/(1+jkr)

Impedenza meccanica = Zam(ka)=rc SD jkr/(1+jkr)

Quando kr è piccolo il denominatore si approssima a uno

Za(kr)=rc jkr = rcr j w/c = jrr w

In questo modo c viene semplificato e per la pressione risulta (perché si semplifica anche r):

p =j r w Q /(4 p r)

il fatto che sia immaginaria indica che a bassa frequenza pressione è in quadratura alla velocità.

Se invece valutiamo Za(kr) per molto grandi (a grande distanza dalla sorgente) risulta che Za è indipendente dalla frequenza e vale rc. Quindi si usano queste due semplificazioni per le basse frequenze e per le grandi distanze.

Walzer usa, per la pressione della sorgente semplice, questa espressione:

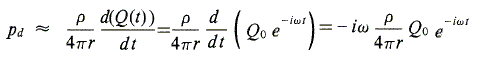
che è la stessa ottenuta qui a meno del segno. Questa si può migliorare inserendo l’espressione di Za(kr) per la sfera pulsante. In questo modo si estense la validità del modello fin quasi ka=1.

In un ambiente domestico le frequenze sono basse e le distanze non sufficienti per le approssimazioni. Ne segue che le simulazioni di REW e di Walzer (riguardo la pressione in ambiente) sono valide per quanto riguarda la distribuzione dei modi ma non per il calcolo della pressione.

Quello che si deve fare è modellare correttamente l’impedenza della sorgente.