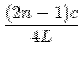Condotto Cilindrico (di lunghezza finita)
Il condotto di
accordo reflex è un tubo aperto ad entrambe le estrremità.
L’impedenza di ingresso (x=0) di un tubo
cilindrivo vale:
(Z0 è l’impedenza per un’onda piana
e ZL l’impedenza del carico)
|
|
= |
|
(15) |
|
|
= |
|
(16) |
L’espressione di ZL è quella di un pistone posto alla fine di un
lungo tubo o di un pistone su parete infinita a seconda del tipo di flangia.
L’impedenza di ingresso di un tubo di lunghezza
finita si stima usando l’approsimazione a bassa frequenza ponendo ZL=0 per tubo aperto o ZL = infinito per un tubo chiuso
In queso caso la (16) diventa:
|
|
per un tubo terminato rigidamente: |
(17) |
|
|
per il
tubo ideale aperto: |
(18) |
A bassa frequenza
![]()
diventa kL e l’impedenza di ingresso si riduce
a:
![]()
Questa è l’espressione dell’impedenza per un tubo
corto e aperto (inertanza acustica).
Similmente per
![]()
la impedenza di ingresso di un tubo rigidamente
terminato diventa:
![]()
che equivale all’impedenza di una cavità chiusa
valida a bassa frequenza.
Eguagliando il tubo aperto in x=0 con il vslore di ZIN=0 nella espressione
precedente, si ottengono le frequenze di risonanza del tubo chiuso ad una
estremità (o-c) e del tubo aperto ad entrambe le estremità (o-o) . Per
![]()
|
tubo chiuso
(open-closed) |
= |
|
(19) |
|
tubo aperto
(open-open) |
= |
|
(20) |
Il tubo chiuso ha una frequenza fondamentale
con lunghezza d’onda pari a 4 volte la lunghezza del tubo stesso e risonanze
più elevate che corrispondono a interi dispari della fondamentale
Il tubo aperto ha la fondamentale corrispondente ad una lunghezza d’onda pari al doppio della lunghezza e le superiori in corrispondenza a tutti i multipli interi della fondamentale.
Per una linea di trasmissione, che è
sostanzialmente un tubo aperto riempito di materiale fonoassorbente, il numero
d’onda k è una quantità complessa ma la forma dell’impedenza non cambia.
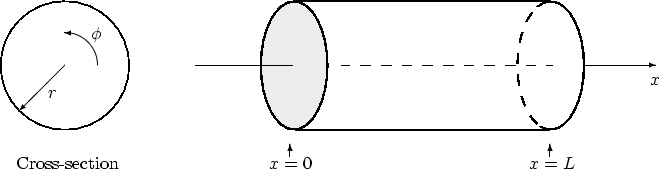
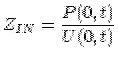
![$\displaystyle Z_{0}\left[\frac{A + B}{A - B}\right]$](./Condotto_file/image003.gif)
![$\displaystyle Z_{0}\left[\frac{Z_{L} \cos (kL) + j Z_{0} \sin(kL)}{jZ_{L} \sin(kL) + Z_{0} \cos(kL)}\right].$](./Condotto_file/image004.gif)