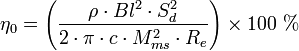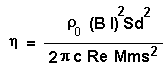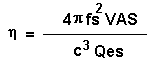Efficienza dell’ altoparlante (dinamico)

di mario Bon

8 ottobre 2015

Il generale l’Efficienza o Rendimento, di un qualsiasi processo che produca lavoro, è il rapporto tra la potenza attiva prodotta e la potenza attiva consumata per ottenerla. Si esprime in parti per cento ed è sempre minore del 100%. Per il calcolo del rendimento si deve fare riferimento al Secondo Principio della Termodinamica.

Le “macchine” con il rendimento più alto sono i trasformatori (rendimento anche superiore 99%).

Potenza_attiva_Ottenuta

Rendimento = Efficienza =100 -------------------------- %

Potenza_attiva_Consumata

Se esistesse una macchina con rendimento del 100% si realizzerebbe il “moto perpetuo” cosa che, fisicamente, contrasta con il Secondo Principio della Termodinamica (ed è impossibile).

L’efficienza e la sensibilità sono due cose diverse e non devono essere confuse.

La sensibilità di un sistema di altoparlanti è data dal livello SPL che esso produce ad un metro di distanza quando si applichi al suo ingresso uno stimolo in tensione pari a 2.83 Vrms (equivalenti a 1 Watt su 8 ohm). La sensibilità quindi è riferita alla tensione applicata all’ ingresso e non alla potenza elettrica che assorbe. Quindi è possibile che una sorgente presenti una sensibilità di 110 dB SPL (magari con impedenza di 1 ohm) mentre è impossibile che emetta più di 109.2 dB SPL con 1 Watt elettrico. In genere si considera la sensibilità associata alla impedenza nominale (ma sarebbe meglio associarla al minimo della parte reale dell’impedenza).

Il Rendimento o Efficienza acustica dell’altoparlante è definita come il rapporto tra la potenza acustica attivaprodotta (PA) e la potenza elettrica attiva assorbita (PE).

Potenza_Acustica_attiva_Ottenuta

Rendimento acustico = Efficienza acustica =100 ----------------------------------- %

Potenza_Elettrica_attiva_Consumata

L’altoparlante dinamico esegue due trasformazioni:

- da segnale elettrico a movimento meccanico

- da movimento meccanico a variazione di pressione (suono).

Dobbiamo quindi definire l’efficienza di due trasformazioni (elettro-meccanica e meccanica-acustica) l’efficienza complessiva è il prodotto delle due.

Efficienza acustica = (efficienza elettro-meccanica) x (efficienza meccanica-acustica)

L‘amplificatore ha una sua impedenza interna. Ne segue che il trasferimento di energia dall’amplificatore al carico dipende anche dalla impedenza interna dell’amplificatore. Per semplificare supponiamo che l’amplificatore sia un generatore di tensione ideale con impedenza interna nulla:

Se l’altoparlante è caricato da una tromba si deve aggiungere un terzo termine:

Efficienza acustica = (efficienza elettro-meccanica)x (efficienza meccanica-acustica)x(efficienza tromba)

Per calcolare il rendimento di un altoparlante è essenziale conoscerne tutti i parametri elettrici, meccanici ed acustici.

Efficienza di un altoparlante per HiFi: tipicamente minore del 2%

Efficienza di un altoparlante per uso professionale (woofer): compresa tra 2% e 6%

“Efficienza” di un altoparlante caricato a tromba: anche superiore al 20%.

L’efficienza di un altoparlante dotato di tromba è così alta perché non viene calcolata applicandi rigorosamente le definizioni.

Efficienza di una sorgente acustica generica alimentata elettricamente:

Una sfera pulsante ideale che emetta 1 Watt acustico su 4p steradianti (tutto lo spazio) produce un livello SPL di 109.2 dB a un metro. Ne segue che, ammesso che la sfera pulsante ideale abbia un rendimento del 100% , emette un Watt acustico in uscita con un Watt elettrico in entrata. Ne segue che nessuna sorgente reale (quindi con rendimento minore del 100%) che emetta su tutto lo spazio può produrre un livello superiore a 109.2 dB riferito a un metro. Si dimostra che qualsiasi sorgente montata in un volume chiuso non può superare il 25% di rendimento (indipendentemente dall’indice di direttività). Si ricorda che i dispositivi passivi (non alimentati) hanno rendimento comunque inferiore al 100% (magari 99.99% ma mai 100%). Le trombe sono dispositivi passivi quindi non aumentano il rendimento della sorgente cui sono applicate: al massimo lo riducono di poco. Le trombe aumentano il livello SPL in una certa zona di spazio. Il calcolo del rendimento va sempre e comunque fatto con le espressioni (1) e (2) riportate nel seguito.

Applichiamo pedissequamente le definizioni:

Potenza_Acustica_attiva_Ottenuta

Rendimento acustico = Efficienza acustica =100 -------------------------------- %

Potenza_Elettrica_attiva_Consumata

La potenza acustica prodotta da una generica sorgente acustica è data dall’espressione 4.20 a pag. 109 di Acoustics di Beranek. Di questa espressione va presa la parte reale (la pressione è una quantità complessa). Al denominatore andrà la potenza elettrica attiva consumata dalla sorgente stessa.

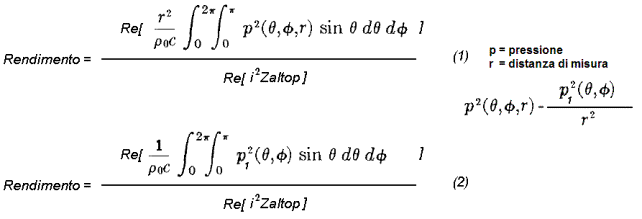
L’espressione (1) vale per qualsiasi superfici di integrazione. L’espressione (2) vale quando la superficie di integrazione è una sfera. In tal caso r è costante e si semplifica. L’espressione (2) risulta quindi indipendente dalla distanza di misura r.

L’ espressione (2) è l’efficienza di una sorgente qualsiasi così come deve essere calcolata. Si notino in particolare gli estremi di integrazione che comprendono tutto lo spazio (4p steradianti) attorno alla sorgente.

Nella (1) e nella (2) non appare esplicitamente la frequenza: in realtà p, e quindi il rendimento, dipende dalla frequenza.

L’impedenza di radiazione della sfera pulsante vale:

jkr

Zrad =rc ---------

1+jkr

dove k è il numero d’onda = w/c ovvero 2pf/c (c=velocità del suono, f=frequenza).

L’impedenza di radiazione della sfera pulsante tende a rc per kr >> 1. Ciò avviene sia per k grande (frequenza alta) sia per R grande (lontano dalla sfera). Questo ragionamento vale, in generale, per qualsiasi sorgente perché a grande distanza i fronti d’onda tendono a diventare piani (raggio di curvatura infinito). Le espressioni (1) e (2) sono quindi valide quando r è abbastanza grande oppure k è abbastanza grande per cui il prodotto kr >>1. Più i fronti d’onda si discostano dalla forma sferica e più si deve aumentare la distanza.

Efficienza dell’altoparlante dinamico:

L’efficienza dell’altoparlante dinamico, riportata in letteratura, è data dalle seguenti espressioni semplificate che non sembrano corrette al 100% (troppe semplificazioni).

l’efficienza è proporzionale al quadrato della superficie di radiazione Sd, al quadrato di (Bl) e inversamente proporzionale alla massa Mms al quadrato. E’ fuori dubbio che si possano scegliere opportuni valori e ottenere efficienza maggiore del 100% (per esempio basta aumentare BL e ridurre RE a parità di massa). Per questo motivo questa espressione non sembra del tutto corretta.

Questa espressione, che dovrebbe essere equivalente alla precedente, è fuorviante perché fs Vas e Qes non sono tra loro ortogonali (dipendono uno dall’altro). In particolare sembra che l’efficienza sia proporzionale a Vas (volume equivalente) cosa che non è: se c’è una cosa che non modifica l’efficienza è proprio la cedevolezza delle sospensioni. Infatti nelle due espressioni precedenti non compare.

L’altoparlante esegue due trasformazioni: da elettrico a meccanico e da meccanico ad acustico. Si devono quindi definire l’ efficienza di queste trasformazioni.

Una prima perdita di efficienza si registra a livello elettrico perché non tutta la potenza viene trasformata in energia cinetica (causa la dissipazione di calore su RE). Ma trascuriamo questo effetto per concentrarci sugli aspetti meccanici e acustici.

Partiamo dalle seguenti definizioni:

Potenza meccanica = Lavoro/tempo = forza x velox (velox=velocità)

Potenza elettrica = Tensione x Corrente

Applichiamo le definizioni ed eseguiamo le debite sostituzioni. Qui di seguito calcoliamo l’efficienza complessa ovvero:

Potenza_Acustica_Ottenuta

Rendimento acustico = Efficienza acustica =100 -------------------------------- %

Potenza_Elettrica_Consumata

Efficienza elettro meccanica	(Potenza_meccanica) ----------------------------- (Potenza_elettrica)	= (forza x velox) / (tensione x corrente) = = (BLiin x velox) / ( iin x vin ) dove BLvelox= vin Zes/(Ze+Zes) velox = velocità dell’apparato mobile	Zes/(Ze+Zes)
Efficienza meccano acustica	(Potenza_acustica) ----------------------------- (Potenza_meccanica)	= p velox/ (forza x velox)= = Re[Za] velox^2/(forza x velox) = Re[Za] velox/forza Zmeccanica= forza /velox	Zaria ------------------ Zmeccanica

 Zaria è la parte reale dell’impedenza di radiazione (Zaria= Re[Za]).

L’efficienza complessa dell’altoparlante è data da

. Zaria Zes

Efficienza = 100 ---------- ------- %

Zmeccanica (Ze+Zes)

Il rapporto Zes/(Ze+Zes) vale 1 se Ze=0. Questo significa che, per aumentare l’efficienza meccanica, si deve ridurre Ze (impedenza della bobina mobile). Per questo motivo si usa dire che l’altoparlante dinamico è un dispositivo sensibile alla corrente.

L’efficienza meccanica si calcola allo stesso modo per qualsiasi tipo di carico (comprese le trombe) a partire dal circuito elettrico equivalente (dove, evidentemente, si devono inserire tutti gli elementi comprese le impedenze di carico).

Vediamo in dettaglio: applicando le definizioni, l’efficienza meccanica risulta essere :

(Potenza meccanica in uscita) (forza x velocità)

Efficienza meccanica = ----------------------------- = ---------------------

(complessa) (Potenza elettrica in ingresso) (tensione x corrente)

(BLi_in x velox)

= ---------------

( i_in x v_in )

La corrente in ingresso appare sia al numeratore che al denominatore e si semplifica. Resta (con le debite sostituzioni):

(BL x velox) v_in Zes/(Ze+Zes) Zes

Efficienza meccanica = ------------- = ----------------- = ------------

v_in v_in (Ze+Zes)

La efficienza acustica si calcola più facilmente e il calcolo è riportato nella tabella

Da cui, moltiplicando per l’efficienza acustica) si ottiene:

Zaria Zes

Efficienza Altoparlante = 100 ------------ x ----- < 100%

Zmeccanica Ze+Zes

Il termine (Zaria/Zmeccanica) indica che, per ottenere un altoparlante efficiente la sua impedenza meccanica deve tendere all’impedenza del carico d’aria sulla superficie del diaframma (massa dinamica molto ridotta).

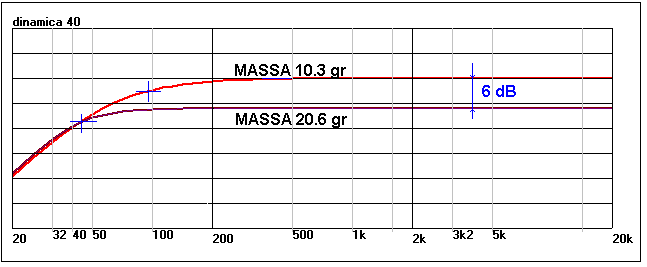
Woofer in cassa chiusa:

Raddoppiando la massa dinamica del woofer, l’efficienza diminuisce (si dimezza) ma aumenta l’estensione verso le basse frequenze (oppure si può ridurre il volume e mantenere la stessa estensione verso il basso.

Volume del cabinet, Sensibilità e banda passante non sono ortogonali: fissate due, la terza viene di conseguenza.

Si noti che l’efficienza elettro-meccanica dell’altoparlante dipende dal carico (cassa chiusa, reflex, tromba…) Il carico altera la velocità dell’apparato mobile alle frequenze più basse e via via sempre meno al crescere della frequenza. Per Ka > 1 il carico cambia poco (la massa di radiazione è piccola rispetto a Mms e la resistenza di radiazione è anche piccola).

Il rendimento “vero” dell’altoparlante è il rapporto delle parti reali della potenza quindi:

Re[BLi_in x velox] Re[BLi_in x velox]

Efficienza meccanica = ------------------ = ---------------

Re[i_in x v_in] Re[i_in² x Z_altop]

Dove Re[] indica la parte reale mentre x indica la moltiplicazione. Scritta così, però, l’espressione non può essere semplificata motivo per cui in letteratura si applicano una serie di semplificazioni.