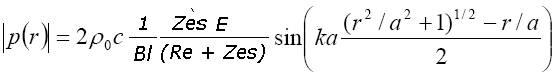SPL di riferimento di un altoparlante dinamico:
Un pistone rigido di raggio a posto su uno schermo infinito produce in asse una pressione p pari a
|
|
Il significato dei simboli è quello solito con k = numero d’onda v=velocità del diaframma r = distanza |
Quando la distanza r è maggiore del raggio moltiplicato per 6 (r > 6 a) l’ espressione della pressione diventa:
|
|
Pressione generata in asse di un pistone rigido di raggio a posto su schermo infinito e a distanza r |
espressione (1) |
Questa espressione deve coincidere con quella che si trova in tutti i testi a partire da Beranek
|
|
Dove E = tensione applicata Sd = superfice del pistone Mmd = massa dinamica SPL= 20 log10(p/prif) con prif=20 10-6 |
Tenendo conto che
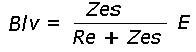
Ad alta frequenza Zes diventa trascurabile rispetto Re (o se si preferisce Ze) e l’espressione si semplifica in:
![]()
Tenendo anche conto che:
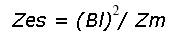
otteniamo l’espressione per la velocità (alle frequenze dove Re >> Zes). In questo range di frequenze Zm dipende praticamente solo dalla massa
e si può scrivere Zm = jwMmd. Dato che interessa il modulo |Zm|=wMmd. Sostituendo e semplificando Bl si ottiene l’espressione per la velocità:
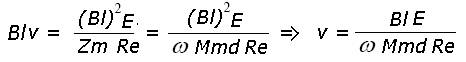
Questa espressione vale quando r>6a, Re>>Zes (o Ze>>Zes) e Zm=jwMmd.
Ora sostituiamo v nella espressione (1) e otteniamo la (2)
Utilizzando l’espressione della velocità possiamo riscrivere l’espressione di Rayleigh come segue:
|
|
|
Espressione generale della pressione generata sull’asse da un pistone rigido di raggio a montato su schermo infinito al variare della distanza r e del raggio del pistone a |
Per rendere questa espressione ancora pià generale basta sostituire Re con Ze (tenendo conto anche dell’induttanza della bobina mobile.
Ricordiamo che questa è l’espressione della pressione in asse (non della potenza acustica).
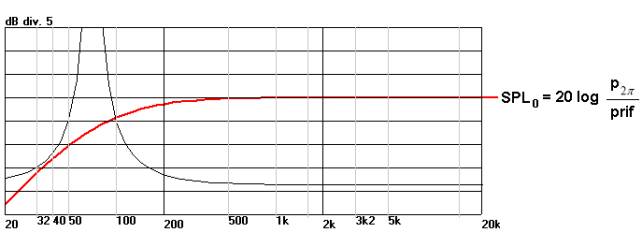
Questo è il significato della SPL di riferimento (si noti che nell’impedenza del woofer non è presente Le).
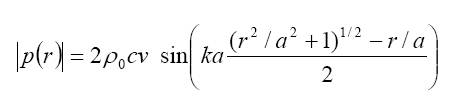
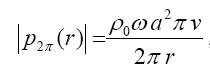
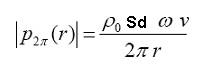
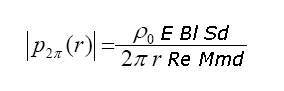 (2)
(2)