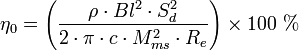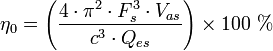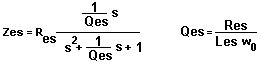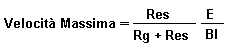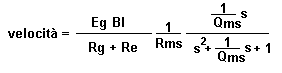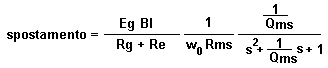Parametri di Small

Small (Parametri di)

Parametri ai piccoli segnali

Sd	Superficie di radiazione in metri quadrati
Mms	Massa del diaframma incluso il carico dell’aria. M_md senza carico dell’aria
Cms	Complinza delle sospensioni.
Rms	Resistenza meccanica (attrito proporzionale alla velocità) in N·s/m
Le	Induttanza della bobina mobile.
Re	Resistenza in continua della bobina mobile
Bl	Fattore di forza (T·m).

	Elettrico	Meccanico	Acustico
Resistenza della bobina mobile in cc	$R E$	$R_{ME} = \frac{(Bl)^2}{R_E}$	$R_{AE} = \frac{(Bl)^2}{R_ES^2_D}$
Massa dinamica	See $C MEC$	$M MD$	$M_{AD} = \frac{M_{MD}}{S^2_D}$
Complicanza delle sostensioni	$L CES$ $= (Bl) 2 C MS$	$C MS$	$C_{AS} = S^2_DC_{MS}$
Perdite viscose	$R_{ES} = \frac{(Bl)^2}{R_{MS}}$	$R MS$	$R_{AS} = \frac{R_{MS}}{S^2_D}$
Complicanza del cabinet	$L_{CEB} = \frac{(Bl)^2C_{AB}}{S^2_D}$	$C_{MB} = \frac{C_{AB}}{S^2_D}$	$C AB$
Perdite del cabinet
$R_{EL} = \frac{(Bl)^2}{S^2_DR_{AL}}$	$R_{ML} = S^2_DR_{AL}$	$R AL$
Massa acustica del condotto	$C_{MEP} = \frac{S^2_DM_{AP}}{(Bl)^2}$	$M_{MP} = S^2_DM_{AP}$	$M AP$
Massa di carico del cabinet
vedere $C MEC$	vedere $M MC$	$M AB$
Massa di radiazione	vedere $C MEC$	Vedere $M MC$	$M A$ $1$

$F_{\rm s} = \frac{1}{2 \pi\cdot\sqrt{C_{\rm ms}\cdot M_{\rm ms}}}$

Qes

$Q_{\rm es} = \frac{2 \pi\cdot F_{\rm s}\cdot M_{\rm ms} \cdot R_{\rm e}}{(Bl)^2}$

Qms

$Q_{\rm ms} = \frac{2 \pi\cdot F_{\rm s}\cdot M_{\rm ms}}{R_{\rm ms}}$

Qts

$Q_{\rm ts} = \frac{Q_{\rm ms} \cdot Q_{\rm es}}{Q_{\rm ms} + Q_{\rm es}}$

VAS

$V_{\rm as} = \rho \cdot c^2 \cdot S_{\rm d}^2 \cdot C_{\rm ms}$

ρ=densità dell’aria (1.184 kg/m³ a 25 °C), c = velocità del suono (346.1 m/s at 25 °C).

Parametri ai grandi segnali

Xmax	Massimo spostamento lineare di picco im mm
Xmech	Massima escursione prima della rottura
Pe	Potenza termica sopportata in Watt.
Sv	Spostamento volumetrico di picco Sv = S_d·X_max
distorsione	Armonica, intermodulazione, ecc.

Altri parametri

Zmax	$Z_{max} = R_e(1+\frac{Q_{ms}}{Q_{es}})$	Massimo di impedenza alla risonanza
EBP	$EBP = \frac{F_s}{Q_{es}}$	Prodotto efficienza per banda passante EBP<50 cassa chiusa (20Hz, 0.35) EBP>100, reflex (40Hz, 0.35)
Znom	4, 8 o 16 ohm	Impedenza nominale (tolleranza 20%)
η₀	$\eta_0 = \left(\frac{\rho \cdot Bl^2 \cdot S_{d}^2}{2 \cdot \pi \cdot c \cdot M_{ms}^2 \cdot R_{e}}\right)\times100\ %$	Efficienza (Potenza disponibile di riferimento) in percentuale. ρ/2πc = 5.445×10^-4 m²·s/kg per ria secca 25 °C. ρ/2πc = 5.365×10^-4 m²·s/kg a 25° e umidità 50%
η₀	$\eta_0 = \left(\frac{4 \cdot \pi^2 \cdot F_s^3 \cdot V_{as}}{c^3 \cdot Q_{es}}\right)\times100\ %$	Come sopra alternativa 4π²/c³ = 9.523×10^–7 s³/m³ per aria secca a 25 °C. 4π²/c³ = 9.438×10⁻⁷ s³/m³. a 25° per umidità 50%
DB (1 watt) SPL rif	SPL@1m/1Watt = 112.1 + 10log(η₀) SPL@1m/2.83Vrms₎ = dB_{(1 watt)} + 10log(8/R_e) = 112.1 + 10log(η₀) + 10log(8/R_e) SPL @1m/1W = 112.1 + 10*log(η₀)	Sensibilità, su schermo infinito a un metro
Compressione	In dB	Indica di quanti dB diminuisce la sensibilità con una certa potenza applicata.

I parametri di Small descrivono e caratterizzano il comportamento dell’altoparlante dinamico.

i parametri meccanici fondamentali (tra loro ortogonali) sono :

piccoli segnali	meccanici	Mms massa
		Cms elesticità o cedevolezza
		Rms smorzamento
		SD superficie di radiazione
	elettrici	RE Resistenza della bobina mobile
		Le Induttanza della bobina mobile
		BL fattore di forza
grandi segnali	meccanici	Xmax spostamento lineare
	elettrici	Massima potenza elettrica applicabile
Parametri dell’altoparlante. I parametri meccanici possono essere considerati tra loro ortogonali. Baterebbe considerare (al posto di Mms) la densità superficiale. I parametri elettrici sono legati tra loro (BL, RE, Le). Anche Xmax e BL dipendono uno dall’altro. Questi elencati in tabella sono i parametri fondamentali del modello semplificato (esistono modelli più evoluti con un numero maggiore i parametri)

Grandezze derivate dal modello semplificato:

fattore di merito meccanico	Qms
fattore di merito elettrico	Qe
fattore di merito totale	Qt
Volume equivalente	VAS
Spostamento volumetrico	SV= Sd Xmax
SPL asintotico	SPL0
Parametri dell’altoparlante. Grandezze derivate. Questi parametri NON sono tra loro ortogonali

I parametri meccanici sono tra loro ortogonali perché la variazione dell’uno non modifica gli altri. Le (induttanza della bobina mobile) dipende dalla frequenza. Le grandezze derivate invece NON sono ortogonali perché la variazione di una di esse modifica anche le altre ( per esempio alterare Qms altera anche Qt).

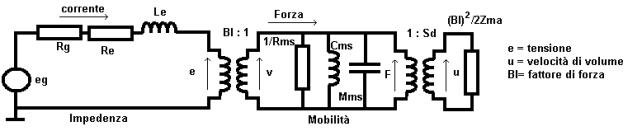
Dato che attraverso le analogie elettroacustiche si definisce un circuito equivalente acustico ed un circuito equivalente elettrico, i parametri fondamentali sembrano moltiplicarsi. In realtà sono sempre gli stessi e, siccome i vari modelli sono tra loro isomorfi, si possono fare tranquillamente tutti i calcoli usando esclusivamente un solo modello.

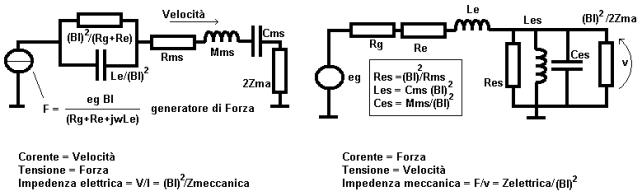
Nota: in questo circuito la velocità corrisponde alla crrente e la forza corrisponde alla tensione . Quindi per coerenza con l’analogia si divrebbe rappresentare lo stimolo con un generatore di velocità (corrente) con l’impedenza Ze verso massa.

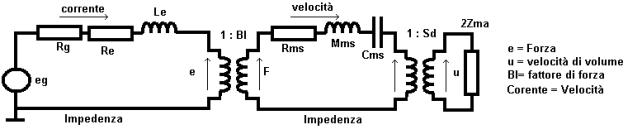
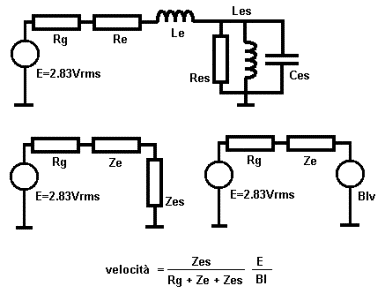
Calcolo della velocità del diaframma di un altoparlante dinamico (in aria o in cassa chiusa) dalla uguaglianza Blv=Zes.

Modello semplificato dove non compare il carico dell’aria.

Z = Ze+Zes è l’impedenza elettrica dell’altoparlante

alla risonanza Zes = Res e Le può essere trascurata per cui la velocità massima è:

Espressioni della velocità e dello spostamento per un altoparlante in aria o cassa chiusa. Per tenere conto dall’induttanza della bobina mobile basta sostituire Re con Ze. La parte dipendente dalla frequenza è normalizzata s = j(w/w₀). Per passare da velocità a spostamento si integra (nel dominio del tempo) nel dominio della frequenza si divide per jw.

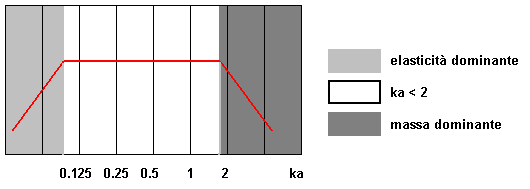
Per un pistone rigido montato su schermo infinito si possono distinguere tre intervalli di frequenza: al di sotto della frequenza di risonanza la risposta è dominata dalla elasticità e cresce di 12 dB/ott, nella zona intermedia per ka<1 la risposta è piatta (perché la parte reale della impedenza di radiazione è crescente) e la regione per ka>1 la risposta è dominata dalla massa e cade di 12 dB/ott. Per 1 < k < 2 c’è una regione di transizione determinata dall’impedenza di radiazione. La forma conica del diaframma dell’altoparlante dinamico provoca un effetto “tromba” che incrementa il livello della emissione. Questo avviene in particolare con i coni in polipropilene che hanno delle rotture progressive e piuttosto dolci.

Nel comportamento dell’altoparlante sono fondamentali le masse: massa del rim , massa dello spider, massa del cono, massa della bobina mobile. Le sospensioni dovrebbero avere massa nulla. Cono e bobina mobile dovrebbero essere perfettamente solidali (invece sono incollate).

Parametri ai grandi segnali

Xmax

Xmech

Massima escursione prima della rottura

Pe

Potenza termica sopportata in Watt.

Sv

Spostamento volumetrico di picco Sv = Sd·Xmax

distorsione

Altri parametri

Zmax

Massimo di impedenza alla risonanza

EBP

Prodotto efficienza per banda passante

EBP<50 cassa chiusa (20Hz, 0.35)

EBP>100, reflex (40Hz, 0.35)

Znom

4, 8 o 16 ohm

Impedenza nominale (tolleranza 20%)

η0

Efficienza (Potenza disponibile di riferimento) in percentuale.

ρ/2πc = 5.445×10-4 m²·s/kg per ria secca 25 °C.

ρ/2πc = 5.365×10-4 m²·s/kg a 25° e umidità 50%

η0

4π2/c3 = 9.523×10–7 s³/m³ per aria secca a 25 °C.

4π2/c3 = 9.438×10−7 s³/m³. a 25° per umidità 50%

DB (1 watt)

SPL rif

Sensibilità, su schermo infinito a un metro

Compressione

Indica di quanti dB diminuisce la sensibilità con una certa potenza applicata.

Parametri dell’altoparlante. Grandezze derivate. Questi parametri NON sono tra loro ortogonali

Spostamento volumetrico di picco Sv = S_d·X_max

η₀

ρ/2πc = 5.445×10^-4 m²·s/kg per ria secca 25 °C.

ρ/2πc = 5.365×10^-4 m²·s/kg a 25° e umidità 50%

η₀

4π²/c³ = 9.523×10^–7 s³/m³ per aria secca a 25 °C.

4π²/c³ = 9.438×10⁻⁷ s³/m³. a 25° per umidità 50%